A definition of a function’s derivative includes the difference quotient formula. The derivative of a function is obtained by taking the limit as the variable h goes to 0 for the difference quotient of the function. The difference quotient, which is frequently used in mathematics, is a metric for determining the average rate of change of a function. Furthermore, calculator-online.net has also introduced the free difference quotient calculator with the help of which it is now possible to carry on complicated difference quotient problems. In the following article, we will learn the procedures for solving the difference quotient and how to use it for geometric interpretation.
Stay Connected!
The formula for Difference Quotient:
y = f(x) has the following formula for the difference quotient:
[ f(x + h) – f(x) ] / h
- F (x + h) is created by changing x in f to x + h. (x)
- The real function is f(x).
The online simplify the difference quotient calculator also utilizes the same formula to depict the results.
Examples:
In the following section, we will try to tie you people with the most relevant examples to understand the concept of the difference quotient.
Statement:
Identify the difference between the function’s f(x) quotient, which is 3x – 5
Solution:
Difference quotient of f(x)
= [ f(x + h) – f(x) ] / h
= [ (3(x + h) – 5) – (3x – 5) ] / h
= [ 3x + 3h – 5 – 3x + 5 ] / h
= [ 3h ] / h
= 3
This is the required answer and can also be verified by using the online simplified difference quotient calculator.
Methods to Solve For Difference Quotient:
An essential concept in mathematics, particularly calculus, is the difference quotient. The difference quotient is the product of the difference between the function values, f(x + h) – f(x), and the difference between the input values, (x + h) – x, given a function f(x) and two input values, x and x + h (where h is the distance between x and x + h).
Difference Quotient = f(x+h) – f(x)/(x+h) – x
As we proceed, the denominator of this may be made simpler since the x cancels out, as you can see in this example.
Difference Quotient Simplified = f(x+h) – f(x)/(x+h) – x = f(x+h) – f(x)/x+h – x
Difference Quotient Simplified = f(x+h) – f(x)/h
The difference quotient is as follows, as we can see:
f(x) (f(x + h)) / h
For calculating the difference quotient, we have a formula. Let’s now think about the actions necessary to solve this difference quotient. Any time we are given a formula, all we need to do to solve it is to identify the values of the variables and expressions it contains, put them in, and then simplify. In order to resolve the difference quotient for a function, f, the following procedures are used (x).
- Simplify to determine f(x + h), and then plug in x + h.
- Once you obtain f(x + h), simplify and insert in f(x + h) and f(x) to find f(x + h) – f(x).
- Add your result from step 2 to the difference quotient’s numerator and simplify.
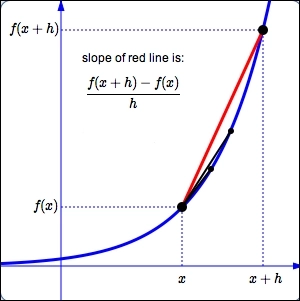
Using Geometry to Interpret:
Okay, so we are aware of the difference quotient’s formula and how to calculate it, but why is this important? Let’s look at the difference quotient’s geometrical meaning to better grasp this.
When we first presented the difference quotient formula,
f(x) (f(x + h)) / h
We described it in terms of two input values, x, and x + h, and a predetermined function, f(x). Let’s give that some thought for a moment. We are studying two points on the function, (x, f(x)) and (x + h, f(x + h), where we have input values of x and x + h. The associated function values, or y-values, are then f(x) and f(x + h).
Using The Difference Quotient Calculator:
The slope of the curved line connecting two points is calculated using an online difference of quotient calculator by following these steps:
- Enter a function (f) that is applicable to any of the variables in the drop-down list.
- To carry on, click the calculate button.
Wrapping It Up:
For calculating the derivative of quotients for different functions, use the difference quotient calculator. Finding the difference quotient would be a simple process as a result. This is one of the straightforward techniques for calculating a function’s quotient. The difference quotient calculator may be used to determine the difference quotient between a linear and quadratic equation.